| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- ADsP요약
- Address translation
- free-space manage
- reverse proxy
- webserver
- MQTT
- was
- 은닉마르코프모델
- memory virtualization
- ADsP
- hmm
- Docker Compose
- RTMP
- CPU virtualization
- docker
- 2025년시작
- TLS
- goroutine
- docker container
- Process
- videostreaming
- InfluxDB
- paging
- 페이징
- segmentation
- rtmpserver
- Today
- Total
Euclidean space
은닉 마르코프 모델 HMM (Hidden Markov Model) 본문
* 패턴인식(오일석) 7장 순차 데이터의 인식의 내용을 학습하고 정리한 글입니다. 모든 그림은 해당 책으로부터 가져왔습니다.
순차 데이터 (Sequential data)
: 시간성(temporary property)를 갖는 데이터
시간성을 갖지 않는 데이터와 대비 시켜보면서 특징을 알아보겠습니다.
① 특징의 순서를 바꾸면 패턴의 물리적 특성이 왜곡된다.

[그림 7.1]은 두 축 x1, x2를 바꾼 공간입니다. 바꾸어도 베이지안 분류기, 신경망, SVM, k-NN 등 문제되지 않습니다.
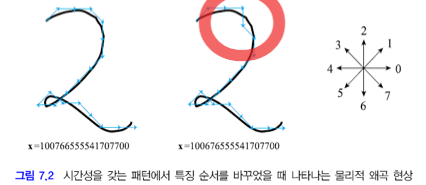
[그림 7.2]는 x4, x5를 바꾼 모습입니다. 이 경우 시간성을 갖는 경우 패턴의 물리적 특성이 왜곡됩니다.
② 특징 벡터가 가변 길이를 갖는다.
③ 관측 벡터로 표현한다.
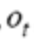
: 시간 t에서의 관측
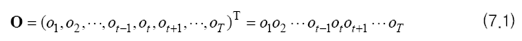
: 관측 벡터 (HMM은 관측이 스칼라이고 이산인 경우)
관측이 이산 값을 가지므로 유한한 개수의 값 중 하나를 갖습니다.
이러한 값의 집합을 알파벳이라고 합니다.
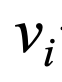
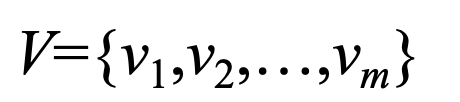
: 알파벳을 구성하는 기호(symbol)
: 알파벳
④ 알파벳을 구성하는 기호들이 시간에 따라 의존성을 갖는다.

[그림 7.2]를 다시 살펴봅시다. t에서 2(↑)가 나타난 뒤 6(↓)이 나타날 확률은 작습니다.
마르코프 사슬 이론
러시아 수학자 안드레이 마르코프는
시간 t에서의 관측은 가장 최근 r개의 관측에만 의존한다고 가정하고
마르코프 사슬 이론을 제시하였습니다.
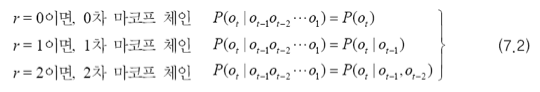
0차 마르코프 체인은 과거에 전혀 의존하지 않는 형태,
1차 마르코프 체인은 이전 관측에만 의존하는 형태,
2차 마르코프 체인은 바로 이전 두 개의 관측에만 의존하는 형태입니다.
(7.2)를 시각적으로 나타내면 아래 그림과 같습니다.
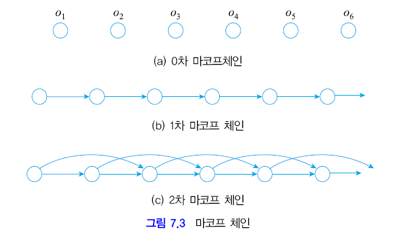
예시를 통해 마르코프 체인을 이해해봅시다.
아래와 같이 최근 3일 간의 날씨 정보가 주어진 경우

오늘 비올 확률은?
1차 마르코프 체인을 활용할 경우
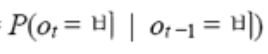
확률은 이와 같이 쓸 수 있습니다.
따라서 1차 마르코프 체인을 활용하는 경우 아래 4개의 확률이 같게 됩니다.
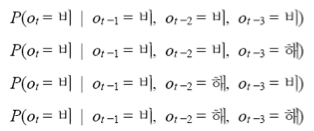
실제로 이 확률이 모두 같을까요?
아닙니다. 내일 비가 올 확률이 '비 -> 비 -> 비' 인 경우가 '비->해->해'인 경우보다 큽니다.
이러한 오차도 괜찮다면 1차 마르코프 체인을 사용하면 됩니다.
마르코프 모델은 1차 마르코프 체인을 사용합니다.
오차를 견딜 만큼 1차 마르코프 체인의 가정에 만족하며, 2차 이상의 마르코프 체인은 추정해야하는 매개 변수가 너무 많기 때문입니다.
마르코프 모델
알파벳이 V일 때 m개의 알파벳을 구성하는 기호가 있습니다.
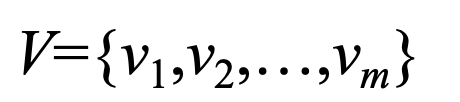
이때 m개의 기호는 상태 state 입니다.
날씨로 예를 들어보면 V = { 비, 구름, 해 } 이며,
비, 구름, 해 3가지 상태입니다.

이 날씨 변화 확률을
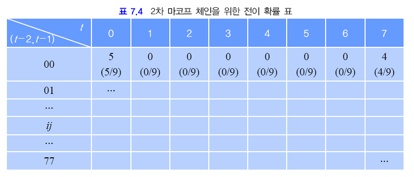
아래 [그림 7.4(a)]처럼 상태 전이 확률 행렬(state transition probability matrix)로 표현할 수 있습니다.

행렬요소는
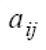
: 상태 vi에서 상태 vj로 이동할 확률
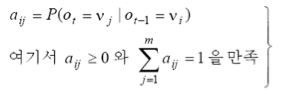
이때 관측 벡터 O의 확률을 아래와 같이 구해볼 수 있습니다.
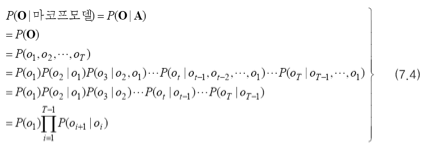
예제를 통해서 실제 계산까지 해봅시다.
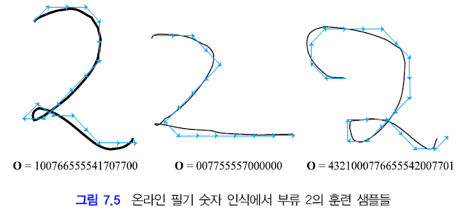
위 예의 상태 전이 횟수들을 아래와 같이 정리할 수 있습니다.
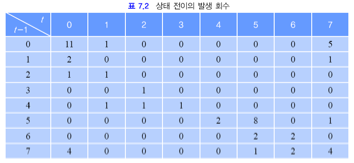
t-1일 때 5, t일 때 4인 경우는 2번 나타났습니다.
이를 상태 전이 확률 행렬로 표현하면 아래와 같습니다.

세 개의 샘플이 t=1일 때, 각각 1, 0, 4입니다. 따라서 초기 확률 벡터는 아래와 같습니다.

상태 전이 확률 행렬과 초기 확률이 있으면 아래 문제를 해결할 수 있습니다.

위와 같이 어떤 샘플이 발생할 확률을 계산할 뿐 아니라,
패턴을 생성하라는 명령에 대해서도 확률 분포를 통해 생성이 가능하기 때문에 마르코프 모델은 생성 모델로도 취급됩니다.
위 예제를 0차 마르코프 체인과 2차 마르코프 체인과 비교해봅시다.
- 0차 마르코프 체인

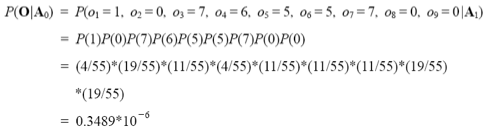
- 2차 마르코프 체인
➡︎ 2차는 훨씬 많은 매개변수 값을 추정해야하며, 계산 복잡도가 크게 증가한다.
추정해야하는 매개변수를 따져봅시다.
m-1개 : 0차
m(m-1)개 : 1차
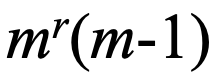
: r차
차수를 늘리면 정확한 모델링이 가능한데 추정할 매개변수가 기하급수적으로 증가합니다.
이렇다보니 마르코프 모델은 능력의 한계가 있습니다.
이를 보완하기 위해 상태들을 감추는 은닉 마르코프 모델(HMM)로 발전하게 됩니다.
HMM은 차수를 미리 고정하지 않고 모델 자체가 확률 프로세스에 따라 정하도록 합니다.
은닉 마르코프 모델
마르코프 모델과 은닉 마르코프 모델을 비교하며 살펴봅시다.

[그림 7.7]에서 보이다시피 (a)마르코프 모델은 상태가 보입니다.
해 -> 해 -> 비 -> 구름이 관측되었다면, s3 -> s3 -> s1 -> s2에서 관측한 결과입니다.
상태가 그대로 보이므로, 당연하게 상태를 알 수 있습니다.
반면 (b)은닉 마르코프 모델은 모든 상태에서 비, 구름, 해가 관측 가능합니다.
해 -> 해 -> 비 -> 구름이 관측되었다면, s3 -> s3 -> s1 -> s2 일 수도 s3 -> s3 -> s1 -> s2 일 수도 있습니다. 가능한 경우는 총 81 ( 3*3*3*3) 가지입니다. 따라서 우리가 관측한 값(해, 비, 구름)으로 상태를 추측해야합니다.
그 중 s3 -> s3 -> s1 -> s2가 관측될 확률을 구한다면 아래와 같습니다.
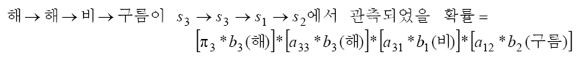
은닉 마르코프 모델의 예제를 살펴봅시다.
예제 7.3) 공을 담은 항아리
항아리에 색깔이 칠해진 공들이 담겨있습니다.
항아리: n개
색깔: m개
n=3, m=4, 항아리에 어떤 공이 담겨있는지 안다고 가정할 때
알파벳 V = {하양, 검정, 연파랑, 진파랑} 입니다.

(b)에서 π는 초기 상태 확률을 의미합니다.
π = [0.5, 0.3, 0.2]
π 항아리에서 카드를 하나 뽑고, 해당 카드 번호의 상태 항아리에서 공을 뽑고 색을 확인하고 다시 넣습니다.
이를 반복합니다.
우리에게 보이는 것은 공의 색깔입니다.
항아리(상태)는 보이지 않습니다.
우리는 공의 색깔(관측값)을 통해 항아리(상태)를 추론할 수 있습니다.
공의 색깔만 알고 있을 때에도, 공이 어떤 항아리에서 나왔는지 추론할 수 있습니다.
이 과정으로 보이지 않는 항아리(은닉 상태)를 공의 색깔(관측값)을 바탕으로 예측할 수 있고, 이것이 바로 은닉 마르코프 모델(HMM)의 핵심입니다.
하지만 이 예제는 현실세계와 다른 이상적인 부분이 있습니다.
바로 항아리 내부에 구성된 공의 정보, 항아리가 몇 개인지 등등을 알고있다는 점입니다.
즉, HMM을 만드는 데 필요한 핵심 정보를 수집할 수 있다는 가정 하에 생각을 해보았습니다.
하지만 현실에선 이 정보들을 알 수 없는 상황이 있을 수도 있습니다.
우리가 관측을 통해 확실히 알 수 있는 것은 공의 색깔입니다.
관측을 충분히 하여 얻은 정보(훈련 데이터)로 HMM을 학습해야 합니다.
바로 위에서 언급해던 문제를 HMM을 실제 응용에 적용하기 위해 생각해봅시다.
이를 위해 우선 HMM을 수학적으로 공식화해봅시다.
아키텍처
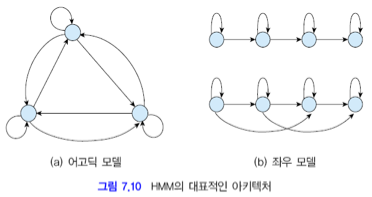
HMM을 가중치 방향 그래프로 표현합니다.
노드는 상태입니다.
모든 노드간에 에지를 갖는 완전 연결 구조도 있고, 아닌 경우도 있습니다.
(a)는 완전 연결 구조인 어고딕 모델
(b)는 상태 전이가 왼쪽에서 오른쪽으로 일어나는 좌우 모델입니다.
매개변수
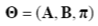
HMM은 세 가지 매개변수를 갖습니다.

: 상태 전이 확률

2.

: 관측 확률
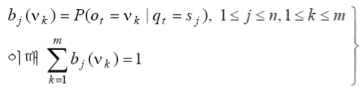
3.
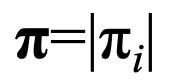
: 초기 상태 확률 벡터
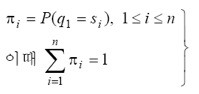
자, 이제 HMM을 응용하기 위해 풀 세 가지 문제를 알아봅시다.
평가와 디코딩은 HMM이 주어진 상황에서 푸는 것,
학습은 훈련 집합이 주어진 상황에서 HMM을 만드는 작업입니다.
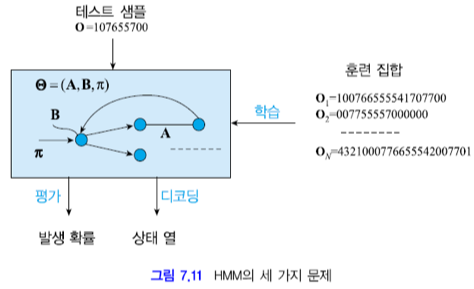
1. 평가
- 모델 Θ가 주어진 상황에서, 관측벡터 O를 얻었을때 P(O| Θ)는?
- ⇨ 주어진 관찰 데이터가 HMM에서의 발생 확률을 계산하는 문제
- DP 알고리즘으로 해결
모델 Θ가 주어진 상황에서 관측벡터 O를 얻었을때, 관측한 상태열을 안다고 가정하면
P(O, Q| Θ)는 아래와 같이 표현할 수 있습니다.
관측과 전이를 반복하는 과정에서 발생하는 확률을 모두 곱한 식입니다.

실제 HMM은 관측벡터 O를 관측한 상태열을 모릅니다.
그 경우 P(O| Θ)는 아래와 같이 표현할 수 있습니다.
가능한 모든 후보 상태열의 확률을 구하고 더하는 식입니다.
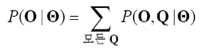
상태가 n개라고 할 때, 가능한 모든 상태열은 n**T개가 됩니다.
확률을 구해야하는 상태열이 너무 많다보니, 계산 폭발이 발생합니다.
이때 DP 알고리즘으로 해결할 수 있습니다.
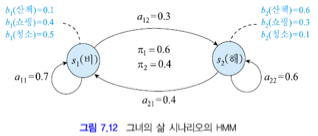
위 그림의 모든 상태열을 보면

Q1, Q2가 비비비비, 비비비해로 '비비비'가 동일하다는 것을 알 수 있습니다.
이런 경우를 고려하여
아래와 같이 순환적으로 계산할 수 있습니다.


관측벡터의 1~t까지 관측하고, 시간 t 상태에 si에 있을 확률입니다.


2. 디코딩
- 모델 Θ가 주어진 상황에서, 관측벡터 O를 얻었을때 최적의 상태열은?
- ⇨ 주어진 관찰 데이터에 대해 가장 가능성 높은 은닉 상태 시퀀스를 찾는 문제
- DP 알고리즘(Viterbi 알고리즘)으로 해결
P(O,Q|Θ)를 기준 함수로 채택하고 이것을 최대화하는 최적 상태열을 찾아야 합니다.

이 경우도 평가 문제처럼 계산 폭발이 일어나기 때문에 DP로 해결할 수 있습니다.
평가 문제와 마찬가지로 모든 Q(상태)에 대해 계산하고, 그 중 가장 큰 값을 취합니다.
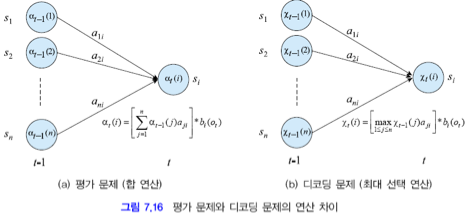
모든 상태를 계산하고, 큰 값을 취하기 위해서
전방 계산을 하고, 역추적하여 경로를 찾아야합니다.

전방 계산으로 T에서 가장 큰 확률을 갖는 상태를 찾습니다. 이를 T-1, T-2, ... , 1 순서대로 역추적합니다.

이 알고리즘을 Viterbi 알고리즘이라고 합니다.
3. 학습
- 훈련집합 X가 주어져 있을때 HMM의 매개 변수 Θ는?
- ⇨ HMM의 매개변수를 최적화하는 문제
- EM 알고리즘 (Baum-Welch 알고리즘)으로 해결

여기서 사용되는 EM 알고리즘은 두 단계로 나뉩니다.
- E 단계 (Expectation 단계): 현재 모델 파라미터로 주어진 관측 데이터가 발생할 확률을 계산
- M 단계 (Maximization 단계): E 단계에서 계산된 값을 사용하여 모델 파라미터를 업데이트

이 단게를 반복하며 매개변수가 업데이트됩니다.
여기까지 은닉마르코프모델에 대해 정리를 해보았는데
틀린 내용이 있다면 알려주세요🐨
감사합니다🍀

